Pseudo random binary sequences (PRBS) show up in many applications such as cryptography and communications, but my main interest in them stems for their use in providing pseudo random data for generating eye pattern diagrams (EPD). Without getting into details on why one would want to generate EPD (see the link above for some of that), one of the issues I’ve been working on lately is how to generate PRBS at very high rates, in excess10 Gigabits per second, economically.
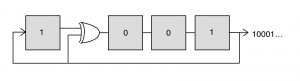
The specific type of PRBS that are used for generating EPD are the so called maximum length sequence (m-sequences) and these are typically generated using linear feedback shift register (LFSR). This is just a chain of flip-flops that is fed back on itself in a specific way to generate the PRBS of interest. To make this concrete, let’s consider a 4-bit LFSR implemented with 4 flip-flops and a xor gate as shown below. This circuit generates a repeating, length-15 series of bits: 100010011010111…
Now an important point is that these flip flips and gates tend to be relatively slow. However, serializers that convert multiple, parallel channels to a single, serial channel at a faster rate are available at quite high data rates (I’ve seen parts rated to above 50 Gbps). This suggests that a way to generate high speed PRBS is to generate multiple bits of the PRBS at a time and then combine them using a serializer. There are at least two approaches to this. One is simply to advance the sequence multiple bits at each clock. This turns out to be practical, although it requires some additional hardware. However, a more interesting, although not necessarily more practical approach, is generate alternating bits in parallel.
This second approach relies on an interesting property of these m-sequences: if one takes every other element of the sequence (this is referred to as decimation by twos), the result is a shifted sequence of the original sequence:
100010011010111100010011010111… ➡ 101011110001001… 100010011010111100010011010111… ➡ 000100110101111…
Examining these two sequences, we see that that both of the resulting sequences are just shifted versions of our original sequence, with the second sequence shifted 7 bits further than the first. With this result in hand, it’s clear that we can generate our sequence at twice the base rate if we combine two LFSR that are shifted by 7 bits with respect to each other.
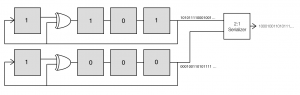
What’s particularly interesting about this is that the circuits to create the two sequences which we feed to the serializer are identical to the original LFSR except that they are initialized to different values. Furthermore, this trick can be extended to combining 4 shifted sequences using a 4:1 MUX by taking every fourth element of the original m-sequence to get shifted versions.
100010011010111100010011010111… ➡ 111100010011010… 100010011010111100010011010111… ➡ 000100110101111… 100010011010111100010011010111… ➡ 001101011110001… 100010011010111100010011010111… ➡ 010111100010011…
In fact, for longer sequences, one can take every 2nth element and always get a shifted version of the original sequence. For example, for a 10 bit LFSR, which can generate a 210-1 or 1023 bit PRBS, we could generate the sequence up to 512 bits at time using this scheme. A more realistic case would probably involve generating the sequence 64 bits at a time (this is the width of the serializers on some FPGAs). However, and this is where the possible impracticality comes in, one would need 640 flip flops as opposed to 10 flip flops for the base LFSR.
This might be acceptable in a pinch, but there is another approach that typically requires less resources. The figure shown below advances the PRBS two time steps for each clock cycle, where the two output bits can be read from the output of the two rightmost flip-flops.
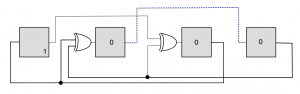
This has the same effect as the two parallel PRBS generators show above, but saves four flip flops. However, things get more complicated when generating a larger number of bits. In that case the signal needs to propagate through multiple xor gates at each clock, possibly slowing the maximum achievable data rate.
Despite the extra resources this takes up, this is an interesting way of exploiting the properties of m-sequences to generate PRBS at faster rates. It may slightly outperform the serial implementation when generating large number of bits at a time, so could be useful for generating very high rate signals. (A hybrid approach could also be envisioned where both techniques are used to reduce resources while preserving the maximum rate; interesting, but a topic for another day.)